经典排序算法的 Python 实现

插入排序

描述

插入排序是通过内外双重循环实现。外部循环按照序列顺序从头到尾依次循环取每个值key，内部循环倒序取值序列中key之前的每个元素。比如，x 为 key 之前的一个元素，如果 x < key ，则交换两者的位置，直到对比交换到第0个元素。插入排序使用双重循环，所以时间复杂度为O(n^2)。是稳定的排序算法。

演示

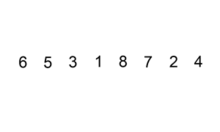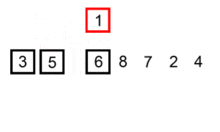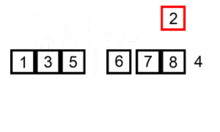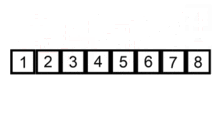
代码实现

def insert_sort(lists):
    count = len(lists)
    for i in range(1, count):
        key = lists[i]
        j = i - 1
        while j >= 0:
            if lists[j] > key:
                lists[j+1] = lists[j]
                lists[j] = key
            j -= 1
    return lists

希尔排序

描述

希尔排序，也称为递减增量排序算法，实质是分组插入排序算法，是插入排序的一种更高效的改进版本。由 Donald Shell 于1959年提出，因而得名。希尔排序是非稳定排序算法。

希尔排序是针对插入排序以下两点性质而提出的改进方法：

• 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
• 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

希尔排序的时间复杂度根据步长选择策略而不同，Donald Shell最初建议步长选择为 n/2 并且对步长取半直到步长达到1。虽然这样取可以比 O(n^2)类的算法（插入排序）更好，但这样仍然有减少平均时间和最差时间的余地。选择其他步长的时间复杂度可参考维基百科中希尔排序的介绍。总体上希尔排序的时间复杂度在 O(nlogn) - O(n^2)。

假设有一组数为 [62 69 36 86 56 95 58 64 90 4 90 43 91 25 49 4 22 2 34 2 69 24]，初始步长为5，将这组数分割为一下形态：

62 69 36 86 56
95 58 64 90 4
90 43 91 25 49
22 2  34 2  69
24

针对每一列做插入排序：

22 2  34 2  4
24 43 36 25 56
62 58 64 86 49
90 69 91 90 69
95

步长递减为2，重新排列：

22 2
34 2
4 24
43 36
25 56
62 58
64 86
49 90
69 91
90 69
95

每列按照插入排序得到：

4  2
22 2
25 24
34 36
43 56
49 58
62 69
64 86
69 90
90 91
95

最后以1步长进行排序（此时就是简单的插入排序了）。最终得到排序数列 [2 2 4 22 24 25 34 36 43 46 56 58 62 64 69 69 86 90 90 91 95]。

代码实现

#!/usr/bin/env python

def shell_sort(lists):
    count = len(lists)
    step = int(round(count/2))
    while step > 0:
        for i in range(step, count):
            j = i
            temp = lists[i]
            while j > 0:
                if lists[j-step] > temp:
                    lists[j] = lists[j-step]
                    lists[j-step] = temp
                j = j - step
        step = int(round(step/2))
    return lists

冒泡排序

描述

冒泡排序（英语：Bubble Sort）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

冒泡排序算法的运作如下：

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

冒泡排序对 n 个项目需要 O(n^2) 的比较次数，时间复杂度为 O(n^2)。

代码实现

#!/usr/bin/env python

def bubble_sort(lists):
    count = len(lists)
    for i in range(count):
        for j in range(1, count-i):
            if lists[j-1] > lists[j]:
                lists[j-1],lists[j] = lists[j],lists[j-1]
    return lists

选择排序

描述

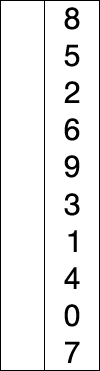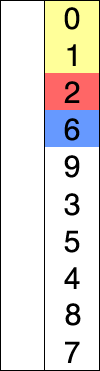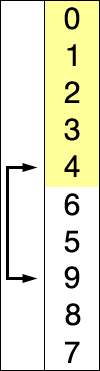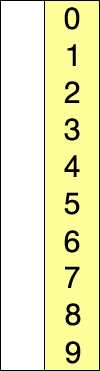
选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

选择排序的时间复杂度为 O(n^2)

演示

代码实现

#!/usr/bin/env python

def selection_sort(lists):
    count = len(lists)

    for i in range(count):
        min = i
        for j in range(i+1, count):
            if lists[j] < lists[min]:
                min = j
        lists[i],lists[min] = lists[min],lists[i]
    return lists

归并排序

描述

归并排序（英语：Merge sort，或mergesort），是创建在归并操作上的一种有效的排序算法，效率为O(n log n)。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。

归并操作（merge），也叫归并算法，指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。

演示

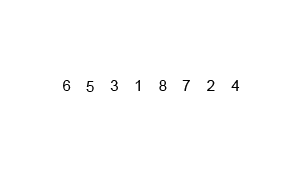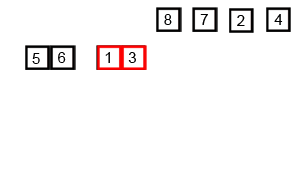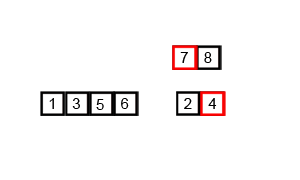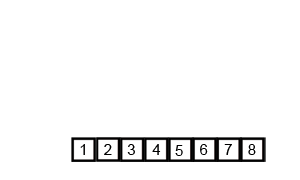
归并排序有两种实现方式：迭代法和递归法

代码实现

#!/usr/bin/env python

"""代码使用递归法实现，引用自维基百科
   https://zh.wikipedia.org/wiki/%E5%BD%92%E5%B9%B6%E6%8E%92%E5%BA%8F#Python
"""

from collections import deque

def merge_sort(lst):
    if len(lst) <= 1:
        return lst

    def merge(left, right):
        merged,left,right = deque(),deque(left),deque(right)
        while left and right:
            merged.append(left.popleft() if left[0] <= right[0] else right.popleft())  # deque popleft is also O(1)
        merged.extend(right if right else left)
        return list(merged)

    middle = int(len(lst) // 2)
    left = merge_sort(lst[:middle])
    right = merge_sort(lst[middle:])
    return merge(left, right)

快速排序

描述

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），一种排序算法，最早由东尼·霍尔提出。在平均状况下，排序n个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他Ο(n log n)算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。

快速排序使用分治法（Divide and conquer）策略来把一个序列（list）分为两个子序列（sub-lists）。

步骤为：

1. 从数列中挑出一个元素，称为”基准”（pivot），
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
   递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

演示

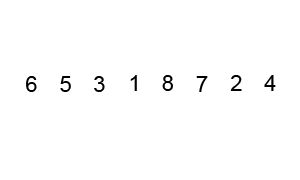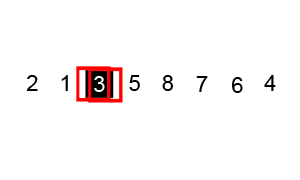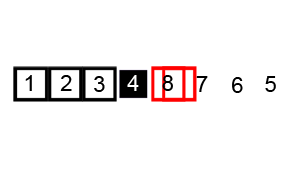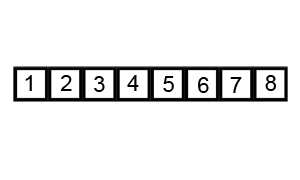
代码实现

#!/usr/bin/env python

def qsort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        return qsort([x for x in arr[1:] if x < pivot]) + \
               [pivot] + \
               qsort([x for x in arr[1:] if x >= pivot])

if __name__ == '__main__':
    lists = [62, 69, 36, 86, 56, 95, 58, 64, 90, 4, 90, 43, 91, 25, 49, 4, 22, 2, 34, 2, 69, 24]
    print qsort(lists)

>>> [2, 2, 4, 4, 22, 24, 25, 34, 36, 43, 49, 56, 58, 62, 64, 69, 69, 86, 90, 90, 91, 95]

堆排序

描述

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

堆结点的访问

• 父节点i的左子节点在位置(2*i+1);
• 父节点i的右子节点在位置(2*i+2);
• 子节点i的父节点在位置floor((i-1)/2);

堆的操作

在堆的数据结构中，堆中的最大值总是位于根节点。堆中定义以下几种操作：

• 最大堆调整（Max_Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
• 创建最大堆（Build_Max_Heap）：将堆所有数据重新排序
• 堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算

演示

代码实现

#!/usr/bin/env python
#-*-coding:utf-8-*-

def heap_sort(lst):
    def sift_down(start, end):
        """最大堆调整"""
        root = start
        while True:
            child = 2 * root + 1
            if child > end:
                break
            if child + 1 <= end and lst[child] < lst[child + 1]:
                child += 1
            if lst[root] < lst[child]:
                lst[root], lst[child] = lst[child], lst[root]
                root = child
            else:
                break

    # 创建最大堆
    for start in xrange((len(lst) - 2) // 2, -1, -1):
        sift_down(start, len(lst) - 1)

    # 堆排序
    for end in xrange(len(lst) - 1, 0, -1):
        lst[0], lst[end] = lst[end], lst[0]
        sift_down(0, end - 1)
    return lst
            
def main():
    l = [9,2,1,7,6,8,5,3,4]
    heap_sort(l)

if __name__ == "__main__":
    main()